Tutorial:
FDTD & GPU
Yee's algorithm
Sources
Materials
Boundary conditions
Near-to far field
Application notes
Chapter 2: Yee's algorithm
To calculate electromagnetic field propagation we want to solve Maxwell's equations that link electric and magnetic field components and its time and space evolution. The basic idea being FDTD technique is a succesive update of electric and magnetic field components that are specially placed in the computational volume as shown on the following image:
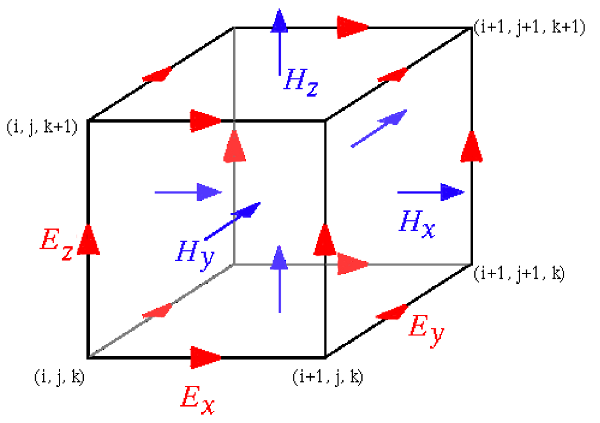
The benefit of this scheme is that we can easily draw a electric field loop around a concrete component of the magnetic field and vice versa. This simplifies the implementation of rotations in the Maxwell equations significantly.
Every computation step has two parts:
- Magnetic field components are updated from electric field components from the previous step.
- Electric field components are updated from magnetic field components.
For update of any component we need only surrounding field values which makes the method suitable for parallelization.
FDTD is a time domain method, so we are always calculating a evolution of electromagnetic field in time. If we want to get a steady state solution, we need to wait a bit (if this helps) or use some other technique that is not time domain, e.g. Finite Element Method.
For Yee algorithm implementation on graphics cards (GPU) in Gsvit, the one-to-one correspondence between GPU threads and computational space points is preserved. The basic data structures are in the GPU global memory; each thread takes the neighbor values (or whatever is necessary for the computation) and after computation updates the value in the global memory again. This approach probably does not use the device memory in an optimum way (shared memory is not used at all), on the other side this keeps the code very simple and fast enough for all the computational space volumes tested. In principle, each thread could computed even more points of the computational volume if necessary; however the size of computational space can be hardly much larger than the maximum number of GPU threads in principle (such data would not fit into the computer RAM).
(c) Petr Klapetek, 2013
